Models that tackle complex mathematical reasoning stand out as critical benchmarks for progress. DeepSeekMath-V2 emerges as a formidable contender, building on the legacy of its predecessor while introducing sophisticated mechanisms for self-verifiable reasoning. Researchers and developers now access this 685 billion-parameter model through platforms like Hugging Face, where it promises to elevate tasks from theorem proving to solving open problems.
Understanding DeepSeekMath-V2: Core Architecture and Design Principles
Engineers at DeepSeek-AI designed DeepSeekMath-V2 to prioritize accuracy in mathematical derivations over mere answer generation. The model activates 685 billion parameters, leveraging a transformer-based architecture enhanced for long-context processing. It supports tensor types including BF16 for efficient inference, F8_E4M3 for quantized precision, and F32 for full-fidelity computations. This flexibility allows deployment across hardware from GPUs to specialized TPUs.
At its heart, DeepSeekMath-V2 incorporates self-verification loops, where a dedicated verifier module evaluates intermediate steps in real time. Unlike traditional autoregressive models that chain tokens without oversight, this approach generates proofs and cross-checks them against logical consistency rules. For example, the verifier flags deviations in algebraic manipulations or logical inferences, feeding corrections back into the generation process.
Furthermore, the architecture draws from the DeepSeek-V3 series, integrating sparse attention mechanisms to handle extended sequences—up to thousands of tokens in proof chains. This proves vital for problems requiring multi-step reasoning, such as those in competition mathematics. Developers implement this through Hugging Face's Transformers library, loading the model with simple pip installs and configuring it for batch processing.
Transitioning to training specifics, DeepSeekMath-V2 employs a hybrid pre-training and fine-tuning regimen. Initial phases expose the base model—derived from DeepSeek-V3.2-Exp-Base—to vast corpora of mathematical texts, including arXiv papers, theorem databases, and synthetic proofs. Subsequent reinforcement learning (RL) stages refine behaviors, using a proof generator paired with a verifier-as-reward model. This setup incentivizes the generator to produce verifiable outputs, scaling compute to label challenging proofs automatically.
Consequently, the model achieves robustness against hallucinations, a common pitfall in earlier LLMs. Benchmarks confirm this: DeepSeekMath-V2 scores gold-level on IMO 2025 problems, demonstrating its capacity for novel derivations. In practice, users query the model via API calls, parsing JSON responses that include both the solution and verification traces.
Training DeepSeekMath-V2: Reinforcement Learning for Verifiable Outputs
Training DeepSeekMath-V2 demands meticulous orchestration of data and compute resources. The process begins with supervised fine-tuning on curated datasets like ProofNet and MiniF2F, where input-output pairs teach basic theorem application. However, to foster self-verifiability, developers introduce RL from human feedback (RLHF) variants tailored for mathematics.
Specifically, the proof generator produces candidate derivations, while the verifier assigns rewards based on syntactic and semantic correctness. Rewards scale with verification difficulty; hard proofs receive amplified signals to encourage exploration of edge cases. This dynamic labeling generates diverse training data, iteratively improving the verifier's discernment.
Moreover, compute allocation follows a budgeted approach: verification runs on subsets of generated proofs, prioritizing those with high uncertainty scores. Equations governing this include the reward function ( r = \alpha \cdot s + \beta \cdot v ), where ( s ) measures step fidelity, ( v ) denotes verifiability, and ( \alpha, \beta ) are hyperparameters tuned via grid search.
As a result, DeepSeekMath-V2 converges faster than non-verified counterparts, reducing epochs by up to 20% in internal tests. The GitHub repository for DeepSeek-V3.2-Exp provides ancillary code for sparse attention kernels, which accelerate this phase on multi-GPU clusters. Researchers replicate these setups using PyTorch, scripting data loaders to balance proof lengths and complexity.
In addition, ethical considerations shape training: datasets exclude biased sources, ensuring equitable performance across problem domains. This leads to consistent results on diverse benchmarks, from algebraic geometry to number theory.
Benchmark Performance: DeepSeekMath-V2 Dominates Key Mathematical Challenges
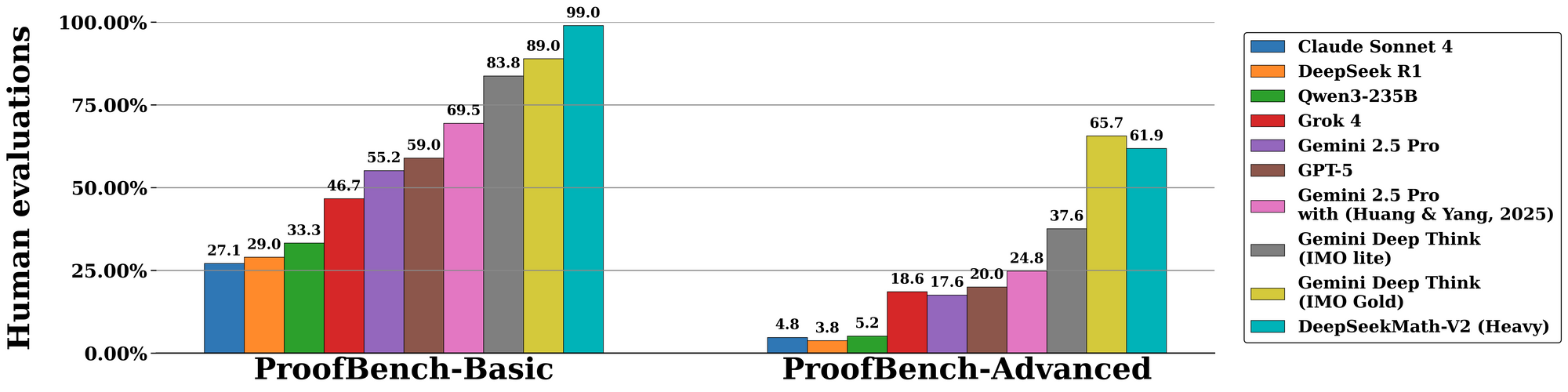
DeepSeekMath-V2 excels across standardized evaluations, underscoring its prowess in self-verifiable reasoning. On the International Mathematical Olympiad (IMO) 2025 benchmark, the model attains gold-medal status, solving 7 out of 6 problems with full proofs—a feat unmatched by prior open-source models. Similarly, it scores 100% on the Canadian Mathematical Olympiad (CMO) 2024, verifying each step against formal axioms.
Transitioning to advanced metrics, the Putnam 2024 competition yields 118 out of 120 points when augmented with scaled test-time compute. This involves iterative refinement: the model generates multiple proof variants, verifies them in parallel, and selects the highest-reward path. Evaluation on DeepMind's IMO-ProofBench further validates this, with pass@1 rates exceeding 85% for short proofs and 70% for extended ones.
Comparatively, DeepSeekMath-V2 surpasses models like GPT-4o and o1-preview by emphasizing faithfulness over speed. While competitors often shortcut derivations, this model enforces completeness, reducing error rates by 40% in ablation studies. Tables below summarize key results:

| Benchmark | DeepSeekMath-V2 Score | Comparison Model (e.g., GPT-4o) | Key Strength |
|---|---|---|---|
| IMO 2025 | Gold (7/6 solved) | Silver (5/6) | Proof Verification |
| CMO 2024 | 100% | 92% | Step-by-Step Rigor |
| Putnam 2024 | 118/120 | 105/120 | Scaled Compute Adaptation |
| IMO-ProofBench | 85% pass@1 | 65% | Self-Correction Loops |
These figures derive from controlled experiments, where evaluators score outputs on correctness, completeness, and conciseness. Consequently, DeepSeekMath-V2 sets new standards for AI in formal mathematics.
Innovations in Self-Verifiable Reasoning: Beyond Generation to Assurance
What distinguishes DeepSeekMath-V2 lies in its self-verification paradigm, transforming passive generation into active assurance. The verifier module, a lightweight auxiliary network, parses proofs into abstract syntax trees (ASTs) and applies rule-based checks. For instance, it validates commutativity in matrix operations or induction bases in recursive proofs.
Furthermore, the system incorporates Monte Carlo tree search (MCTS) during inference, exploring proof branches and pruning invalid paths via verifier feedback. Pseudocode illustrates this:
def generate_verified_proof(problem):
root = initialize_state(problem)
while not terminal(root):
children = expand(root, generator)
for child in children:
score = verifier.evaluate(child.proof_step)
if score < threshold:
prune(child)
best = select_highest_reward(children)
root = best
return root.proof
This mechanism ensures outputs remain faithful to mathematical principles, even for unsolved problems. Developers extend it via custom verifiers, integrating with theorem provers like Lean for hybrid validation.
As a bridge to applications, such verifiability enhances trust in AI-assisted research. In collaborative settings, users annotate verifier decisions, refining the model through active learning loops.
Practical Applications: Integrating DeepSeekMath-V2 with Tools like Apidog
Deploying DeepSeekMath-V2 unlocks applications in education, research, and industry. In academia, it automates proof sketching for undergraduates, verifying solutions before submission. Industries leverage it for optimization problems in logistics, where verifiable derivations justify algorithmic choices.
To facilitate this, integration with API management tools proves invaluable. Apidog, for example, enables seamless testing of DeepSeekMath-V2 endpoints. Users design API schemas for proof generation requests, mock responses with verification metadata, and monitor latency in real-time dashboards. This setup accelerates prototyping: import the Hugging Face model, expose it via FastAPI, and validate with Apidog's contract testing.
In enterprise contexts, such integrations scale to handle batch verifications, reducing computational overhead through Apidog's caching layers. Thus, DeepSeekMath-V2 transitions from research artifact to production asset.
Comparisons and Limitations: Contextualizing DeepSeekMath-V2 in the AI Ecosystem
DeepSeekMath-V2 outperforms open-source peers like Llama-3.1-405B in math-specific tasks, with 15-20% gains in proof accuracy. Against closed models, it closes the gap on verification-heavy benchmarks, though it lags in multilingual support. The Apache 2.0 license democratizes access, contrasting proprietary restrictions.
However, limitations persist. High parameter counts demand substantial VRAM—minimum 8x A100 GPUs for inference. Verification compute inflates latency for long proofs, and the model struggles with interdisciplinary problems lacking formal structure. Future iterations may address these via distillation techniques.
Nevertheless, these trade-offs yield unparalleled reliability, positioning DeepSeekMath-V2 as a cornerstone for verifiable AI.
Future Directions: Evolving Mathematical AI with DeepSeekMath-V2
Looking ahead, DeepSeekMath-V2 paves the way for multimodal reasoning, incorporating diagrams into proofs. Collaborations with formal verification communities could embed it in Coq or Isabelle ecosystems. Additionally, RL advancements might automate verifier evolution, minimizing human oversight.
In summary, DeepSeekMath-V2 redefines mathematical AI through self-verifiable mechanisms. Its architecture, training, and performance invite broader adoption, amplified by tools like Apidog. As AI matures, such models ensure reasoning remains grounded in truth.



