Modelos que abordam o raciocínio matemático complexo se destacam como referências cruciais para o progresso. O DeepSeekMath-V2 surge como um forte concorrente, construindo sobre o legado de seu predecessor enquanto introduz mecanismos sofisticados para o raciocínio auto-verificável. Pesquisadores e desenvolvedores agora acessam este modelo de 685 bilhões de parâmetros através de plataformas como o Hugging Face, onde ele promete elevar tarefas desde a prova de teoremas até a resolução de problemas abertos.
Compreendendo o DeepSeekMath-V2: Arquitetura Central e Princípios de Design
Os engenheiros da DeepSeek-AI projetaram o DeepSeekMath-V2 para priorizar a precisão nas derivações matemáticas em vez da mera geração de respostas. O modelo ativa 685 bilhões de parâmetros, aproveitando uma arquitetura baseada em transformer aprimorada para processamento de contexto longo. Ele suporta tipos de tensores, incluindo BF16 para inferência eficiente, F8_E4M3 para precisão quantizada e F32 para cálculos de fidelidade total. Essa flexibilidade permite a implantação em hardware, desde GPUs até TPUs especializadas.
Em sua essência, o DeepSeekMath-V2 incorpora loops de auto-verificação, onde um módulo verificador dedicado avalia os passos intermediários em tempo real. Ao contrário dos modelos autorregressivos tradicionais que encadeiam tokens sem supervisão, essa abordagem gera provas e as verifica em relação às regras de consistência lógica. Por exemplo, o verificador sinaliza desvios em manipulações algébricas ou inferências lógicas, alimentando correções de volta ao processo de geração.
Além disso, a arquitetura se baseia na série DeepSeek-V3, integrando mecanismos de atenção esparsa para lidar com sequências estendidas — até milhares de tokens em cadeias de prova. Isso se mostra vital para problemas que exigem raciocínio em várias etapas, como aqueles em matemática competitiva. Os desenvolvedores implementam isso através da biblioteca Transformers do Hugging Face, carregando o modelo com instalações pip simples e configurando-o para processamento em lote.
Transitando para as especificidades do treinamento, o DeepSeekMath-V2 emprega um regime híbrido de pré-treinamento e ajuste fino. As fases iniciais expõem o modelo base — derivado do DeepSeek-V3.2-Exp-Base — a vastos corpora de textos matemáticos, incluindo artigos do arXiv, bancos de dados de teoremas e provas sintéticas. As etapas subsequentes de aprendizado por reforço (RL) refinam os comportamentos, usando um gerador de provas emparelhado com um modelo verificador-como-recompensa. Essa configuração incentiva o gerador a produzir saídas verificáveis, escalando a computação para rotular provas desafiadoras automaticamente.
Consequentemente, o modelo alcança robustez contra alucinações, uma armadilha comum em LLMs anteriores. Benchmarks confirmam isso: o DeepSeekMath-V2 atinge nível ouro em problemas da IMO 2025, demonstrando sua capacidade para novas derivações. Na prática, os usuários consultam o modelo via chamadas de API, analisando respostas JSON que incluem tanto a solução quanto os rastros de verificação.
Treinando o DeepSeekMath-V2: Aprendizado por Reforço para Saídas Verificáveis
O treinamento do DeepSeekMath-V2 exige uma orquestração meticulosa de dados e recursos computacionais. O processo começa com o ajuste fino supervisionado em conjuntos de dados curados como ProofNet e MiniF2F, onde pares de entrada-saída ensinam a aplicação básica de teoremas. No entanto, para promover a auto-verificabilidade, os desenvolvedores introduzem variantes de RL a partir de feedback humano (RLHF) adaptadas para a matemática.
Especificamente, o gerador de provas produz derivações candidatas, enquanto o verificador atribui recompensas com base na correção sintática e semântica. As recompensas são escaladas com a dificuldade de verificação; provas difíceis recebem sinais amplificados para encorajar a exploração de casos extremos. Essa rotulagem dinâmica gera dados de treinamento diversos, melhorando iterativamente o discernimento do verificador.
Além disso, a alocação de computação segue uma abordagem orçamentada: a verificação é executada em subconjuntos de provas geradas, priorizando aquelas com altas pontuações de incerteza. As equações que regem isso incluem a função de recompensa ( r = \alpha \cdot s + \beta \cdot v ), onde ( s ) mede a fidelidade do passo, ( v ) denota a verificabilidade, e ( \alpha, \beta ) são hiperparâmetros ajustados via busca em grade.
Como resultado, o DeepSeekMath-V2 converge mais rapidamente do que seus equivalentes não verificados, reduzindo as épocas em até 20% em testes internos. O repositório GitHub para DeepSeek-V3.2-Exp fornece código auxiliar para kernels de atenção esparsa, que aceleram esta fase em clusters multi-GPU. Pesquisadores replicam essas configurações usando PyTorch, roteirizando carregadores de dados para equilibrar os tamanhos e a complexidade das provas.
Além disso, considerações éticas moldam o treinamento: os conjuntos de dados excluem fontes tendenciosas, garantindo um desempenho equitativo em diversos domínios de problemas. Isso leva a resultados consistentes em vários benchmarks, desde geometria algébrica até teoria dos números.
Desempenho de Benchmark: DeepSeekMath-V2 Domina Desafios Matemáticos Chave
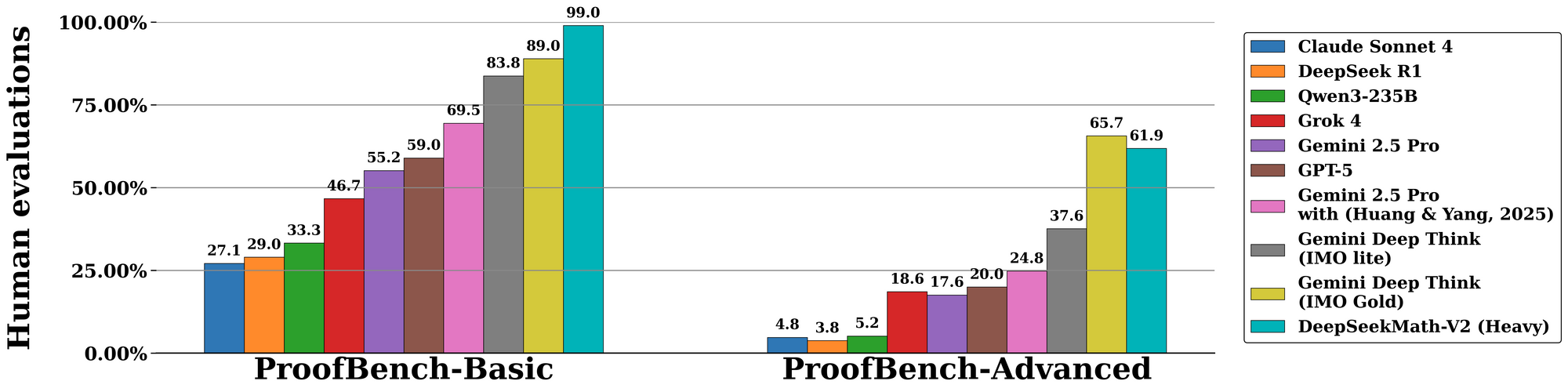
O DeepSeekMath-V2 se destaca em avaliações padronizadas, ressaltando sua destreza no raciocínio auto-verificável. No benchmark da Olimpíada Internacional de Matemática (IMO) 2025, o modelo alcança o status de medalha de ouro, resolvendo 7 de 6 problemas com provas completas — um feito inigualável por modelos de código aberto anteriores. Da mesma forma, ele marca 100% na Olimpíada Canadense de Matemática (CMO) 2024, verificando cada etapa contra axiomas formais.
Transitando para métricas avançadas, a competição Putnam 2024 rende 118 de 120 pontos quando aumentada com computação escalada em tempo de teste. Isso envolve refinamento iterativo: o modelo gera múltiplas variantes de prova, as verifica em paralelo e seleciona o caminho de maior recompensa. A avaliação no IMO-ProofBench da DeepMind valida ainda mais isso, com taxas de pass@1 excedendo 85% para provas curtas e 70% para as estendidas.
Comparativamente, o DeepSeekMath-V2 supera modelos como GPT-4o e o1-preview, enfatizando a fidelidade em detrimento da velocidade. Enquanto os concorrentes frequentemente encurtam as derivações, este modelo impõe a completude, reduzindo as taxas de erro em 40% em estudos de ablação. As tabelas abaixo resumem os resultados chave:

| Benchmark | Pontuação DeepSeekMath-V2 | Modelo de Comparação (ex: GPT-4o) | Principal Vantagem |
|---|---|---|---|
| IMO 2025 | Ouro (7/6 resolvidos) | Prata (5/6) | Verificação de Prova |
| CMO 2024 | 100% | 92% | Rigor Passo a Passo |
| Putnam 2024 | 118/120 | 105/120 | Adaptação de Computação Escalada |
| IMO-ProofBench | 85% pass@1 | 65% | Loops de Auto-Correção |
Esses números derivam de experimentos controlados, onde avaliadores pontuam as saídas em correção, completude e concisão. Consequentemente, o DeepSeekMath-V2 estabelece novos padrões para a IA na matemática formal.
Inovações no Raciocínio Auto-Verificável: Além da Geração para a Garantia
O que distingue o DeepSeekMath-V2 reside em seu paradigma de auto-verificação, transformando a geração passiva em garantia ativa. O módulo verificador, uma rede auxiliar leve, analisa provas em árvores de sintaxe abstrata (ASTs) e aplica verificações baseadas em regras. Por exemplo, ele valida a comutatividade em operações matriciais ou bases de indução em provas recursivas.
Além disso, o sistema incorpora busca em árvore de Monte Carlo (MCTS) durante a inferência, explorando ramos de prova e podando caminhos inválidos via feedback do verificador. Pseudocódigo ilustra isso:
def generate_verified_proof(problem):
root = initialize_state(problem)
while not terminal(root):
children = expand(root, generator)
for child in children:
score = verifier.evaluate(child.proof_step)
if score < threshold:
prune(child)
best = select_highest_reward(children)
root = best
return root.proof
Esse mecanismo garante que as saídas permaneçam fiéis aos princípios matemáticos, mesmo para problemas não resolvidos. Os desenvolvedores o estendem via verificadores personalizados, integrando-se com provadores de teoremas como Lean para validação híbrida.
Como ponte para aplicações, tal verificabilidade aumenta a confiança na pesquisa assistida por IA. Em ambientes colaborativos, os usuários anotam as decisões do verificador, refinando o modelo através de loops de aprendizado ativo.
Aplicações Práticas: Integrando o DeepSeekMath-V2 com Ferramentas como o Apidog
A implantação do DeepSeekMath-V2 abre aplicações em educação, pesquisa e indústria. Na academia, ele automatiza o rascunho de provas para graduandos, verificando soluções antes da submissão. Indústrias o aproveitam para problemas de otimização em logística, onde derivações verificáveis justificam escolhas algorítmicas.
Para facilitar isso, a integração com ferramentas de gerenciamento de API se mostra inestimável. O Apidog, por exemplo, permite o teste contínuo de endpoints do DeepSeekMath-V2. Os usuários projetam esquemas de API para solicitações de geração de provas, simulam respostas com metadados de verificação e monitoram a latência em painéis em tempo real. Essa configuração acelera a prototipagem: importe o modelo Hugging Face, exponha-o via FastAPI e valide com o teste de contrato do Apidog.
Em contextos empresariais, tais integrações escalam para lidar com verificações em lote, reduzindo a sobrecarga computacional através das camadas de cache do Apidog. Assim, o DeepSeekMath-V2 transiciona de artefato de pesquisa para ativo de produção.
Comparações e Limitações: Contextualizando o DeepSeekMath-V2 no Ecossistema de IA
O DeepSeekMath-V2 supera pares de código aberto como o Llama-3.1-405B em tarefas matemáticas específicas, com ganhos de 15-20% na precisão da prova. Contra modelos fechados, ele reduz a lacuna em benchmarks que dependem fortemente de verificação, embora esteja atrasado no suporte multilíngue. A licença Apache 2.0 democratiza o acesso, contrastando com restrições proprietárias.
No entanto, as limitações persistem. Altas contagens de parâmetros exigem VRAM substancial — um mínimo de 8 GPUs A100 para inferência. A computação de verificação aumenta a latência para provas longas, e o modelo tem dificuldades com problemas interdisciplinares que carecem de estrutura formal. Futuras iterações podem abordar essas questões por meio de técnicas de destilação.
No entanto, esses trade-offs resultam em confiabilidade incomparável, posicionando o DeepSeekMath-V2 como um pilar para a IA verificável.
Direções Futuras: Evoluindo a IA Matemática com o DeepSeekMath-V2
Olhando para o futuro, o DeepSeekMath-V2 abre caminho para o raciocínio multimodal, incorporando diagramas em provas. Colaborações com comunidades de verificação formal poderiam incorporá-lo em ecossistemas Coq ou Isabelle. Além disso, avanços em RL podem automatizar a evolução do verificador, minimizando a supervisão humana.
Em resumo, o DeepSeekMath-V2 redefine a IA matemática através de mecanismos auto-verificáveis. Sua arquitetura, treinamento e desempenho convidam a uma adoção mais ampla, amplificada por ferramentas como o Apidog. À medida que a IA amadurece, tais modelos garantem que o raciocínio permaneça fundamentado na verdade.
