複雑な数学的推論に取り組むモデルは、進歩のための重要なベンチマークとして際立っています。DeepSeekMath-V2は、その前身の遺産の上に築かれ、自己検証可能な推論のための洗練されたメカニズムを導入することで、手ごわい競争相手として登場しました。研究者や開発者は現在、Hugging Faceのようなプラットフォームを通じてこの6,850億パラメータモデルにアクセスしており、定理の証明から未解決問題の解決まで、さまざまなタスクを向上させることが期待されています。
DeepSeekMath-V2を理解する:コアアーキテクチャと設計原則
DeepSeek-AIのエンジニアは、DeepSeekMath-V2を単なる回答生成よりも数学的導出の精度を優先するように設計しました。このモデルは6,850億個のパラメータを活性化し、長文コンテキスト処理のために強化されたトランスフォーマーベースのアーキテクチャを活用しています。効率的な推論のためのBF16、量子化された精度を担うF8_E4M3、完全な忠実度計算のためのF32を含むテンソルタイプをサポートしています。この柔軟性により、GPUから特殊なTPUまで、さまざまなハードウェアでのデプロイが可能になります。
DeepSeekMath-V2の核となるのは、自己検証ループです。専用の検証モジュールが中間ステップをリアルタイムで評価します。監視なしでトークンを連鎖させる従来の自己回帰モデルとは異なり、このアプローチは証明を生成し、論理的な一貫性ルールと照合してクロスチェックします。例えば、検証器は代数的操作や論理的推論における逸脱を検出し、その修正を生成プロセスにフィードバックします。
さらに、このアーキテクチャはDeepSeek-V3シリーズから派生しており、スパースアテンションメカニズムを統合して、証明チェーン内の数千ものトークンに及ぶ長大なシーケンスを処理します。これは、競技数学における問題のように、多段階の推論を必要とする問題にとって極めて重要です。開発者はこれをHugging FaceのTransformersライブラリを通じて実装し、簡単なpipインストールでモデルをロードし、バッチ処理用に構成します。
トレーニングの詳細に移ると、DeepSeekMath-V2はハイブリッドな事前学習とファインチューニングのレジメンを採用しています。初期段階では、DeepSeek-V3.2-Exp-Baseから派生したベースモデルを、arXiv論文、定理データベース、合成証明などの膨大な数学テキストコーパスに公開します。その後の強化学習(RL)段階では、証明ジェネレーターと報酬としての検証器モデルを組み合わせて挙動を洗練します。この設定により、ジェネレーターは検証可能な出力を生成するように促され、計算をスケーリングして困難な証明を自動的にラベル付けします。
その結果、このモデルは以前のLLMでよく見られた幻覚に対する堅牢性を達成しています。ベンチマークによってこれが裏付けられており、DeepSeekMath-V2はIMO 2025の問題でゴールドレベルのスコアを獲得し、新しい導出能力を示しています。実際には、ユーザーはAPIコールを介してモデルにクエリを実行し、解決策と検証トレースの両方を含むJSON応答を解析します。
DeepSeekMath-V2のトレーニング:検証可能な出力のための強化学習
DeepSeekMath-V2のトレーニングには、データと計算リソースの綿密な調整が求められます。プロセスは、ProofNetやMiniF2Fのような厳選されたデータセットに対する教師ありファインチューニングから始まり、入出力ペアが基本的な定理の適用を教えます。しかし、自己検証可能性を促進するために、開発者は数学に特化した人間からのフィードバックによる強化学習(RLHF)バリアントを導入しています。
具体的には、証明ジェネレーターが候補となる導出を生成し、検証器は構文的および意味的な正しさに基づいて報酬を割り当てます。報酬は検証の難易度に応じて変動します。難しい証明には、エッジケースの探索を促すために増幅されたシグナルが与えられます。この動的なラベリングにより、多様なトレーニングデータが生成され、検証器の識別能力が繰り返し向上します。
さらに、計算リソースの割り当ては予算制のアプローチに従います。検証は生成された証明のサブセットに対して実行され、不確実性スコアが高いものが優先されます。これを支配する方程式には報酬関数 ( r = \alpha \cdot s + \beta \cdot v ) が含まれ、ここで ( s ) はステップの忠実度を測定し、( v ) は検証可能性を示し、( \alpha, \beta ) はグリッドサーチによって調整されるハイパーパラメータです。
その結果、DeepSeekMath-V2は非検証の同等品よりも速く収束し、内部テストではエポック数を最大20%削減します。DeepSeek-V3.2-ExpのGitHubリポジトリは、スパースアテンションカーネル用の補助コードを提供しており、これによりマルチGPUクラスター上でのこのフェーズが加速されます。研究者はPyTorchを使用してこれらのセットアップを再現し、データローダーをスクリプト化して証明の長さと複雑さのバランスを取っています。
さらに、倫理的考慮事項がトレーニングを形作っています。データセットには偏った情報源が含まれておらず、問題領域全体で公平なパフォーマンスを保証しています。これにより、代数幾何学から数論まで、多様なベンチマークで一貫した結果が得られています。
ベンチマーク性能:DeepSeekMath-V2が主要な数学的課題を圧倒
DeepSeekMath-V2は標準化された評価全体で優れた成績を収め、自己検証可能な推論におけるその実力を示しています。国際数学オリンピック(IMO)2025のベンチマークでは、モデルは完全な証明付きで6問中7問を解決し、金メダルを獲得しました。これは、以前のオープンソースモデルでは達成できなかった偉業です。同様に、カナダ数学オリンピック(CMO)2024では100%のスコアを記録し、各ステップを形式的な公理に対して検証しました。
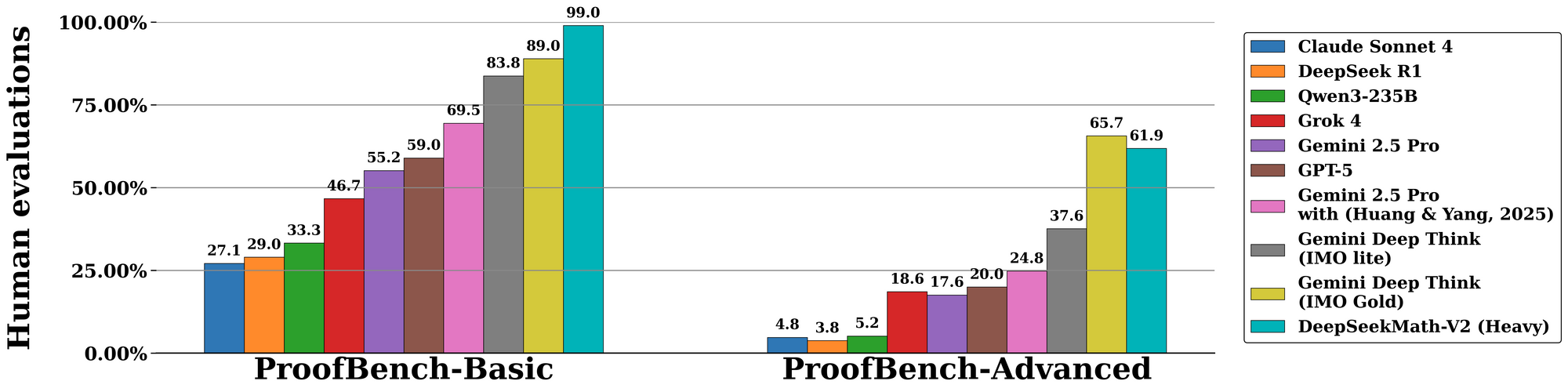
高度なメトリクスに移行すると、Putnam 2024コンペティションでは、スケールアップされたテスト時計算を追加することで、120点中118点を獲得しました。これには反復的な改良が含まれます。モデルは複数の証明バリアントを生成し、それらを並行して検証し、最も報酬の高いパスを選択します。DeepMindのIMO-ProofBenchでの評価はこれをさらに裏付けており、短い証明では85%以上、長い証明では70%以上のpass@1レートを記録しています。
比較すると、DeepSeekMath-V2は速度よりも忠実性を重視することで、GPT-4oやo1-previewのようなモデルを凌駕しています。競合モデルが導出をしばしば短縮するのに対し、このモデルは完全性を強制し、アブレーション研究ではエラー率を40%削減しています。以下の表に主要な結果をまとめます。

| ベンチマーク | DeepSeekMath-V2スコア | 比較モデル(例:GPT-4o) | 主要な強み |
|---|---|---|---|
| IMO 2025 | ゴールド(7/6解決) | シルバー(5/6) | 証明検証 |
| CMO 2024 | 100% | 92% | ステップバイステップの厳密さ |
| Putnam 2024 | 118/120 | 105/120 | スケールされた計算適応 |
| IMO-ProofBench | 85% pass@1 | 65% | 自己修正ループ |
これらの数値は、評価者が正確性、完全性、簡潔性に基づいて出力を採点する管理された実験から導き出されたものです。結果として、DeepSeekMath-V2は形式数学におけるAIの新しい基準を確立しています。
自己検証可能な推論における革新:生成を超え、保証へ
DeepSeekMath-V2を際立たせているのは、その自己検証パラダイムであり、受動的な生成を能動的な保証へと変革します。検証モジュールは、軽量な補助ネットワークであり、証明を抽象構文木(AST)に解析し、ルールベースのチェックを適用します。例えば、行列演算における交換法則や、再帰的証明における帰納法の基底を検証します。
さらに、このシステムは推論中にモンテカルロ木探索(MCTS)を組み込み、証明の枝を探索し、検証器からのフィードバックによって無効なパスを剪定します。擬似コードはこれを説明しています:
def generate_verified_proof(problem):
root = initialize_state(problem)
while not terminal(root):
children = expand(root, generator)
for child in children:
score = verifier.evaluate(child.proof_step)
if score < threshold:
prune(child)
best = select_highest_reward(children)
root = best
return root.proof
このメカニズムは、未解決の問題であっても、出力が数学的原則に忠実であることを保証します。開発者は、カスタム検証器を介してこれを拡張し、ハイブリッド検証のためにLeanのような定理証明器と統合しています。
アプリケーションへの架け橋として、このような検証可能性はAI支援研究への信頼を高めます。共同作業環境では、ユーザーは検証器の決定にアノテーションを付け、アクティブラーニングループを通じてモデルを洗練させます。
実践的な応用:DeepSeekMath-V2とApidogのようなツールとの統合
DeepSeekMath-V2の展開は、教育、研究、産業におけるアプリケーションを解き放ちます。学術界では、大学生向けの証明のスケッチを自動化し、提出前に解決策を検証します。産業界では、物流における最適化問題に活用されており、検証可能な導出によってアルゴリズムの選択が正当化されます。
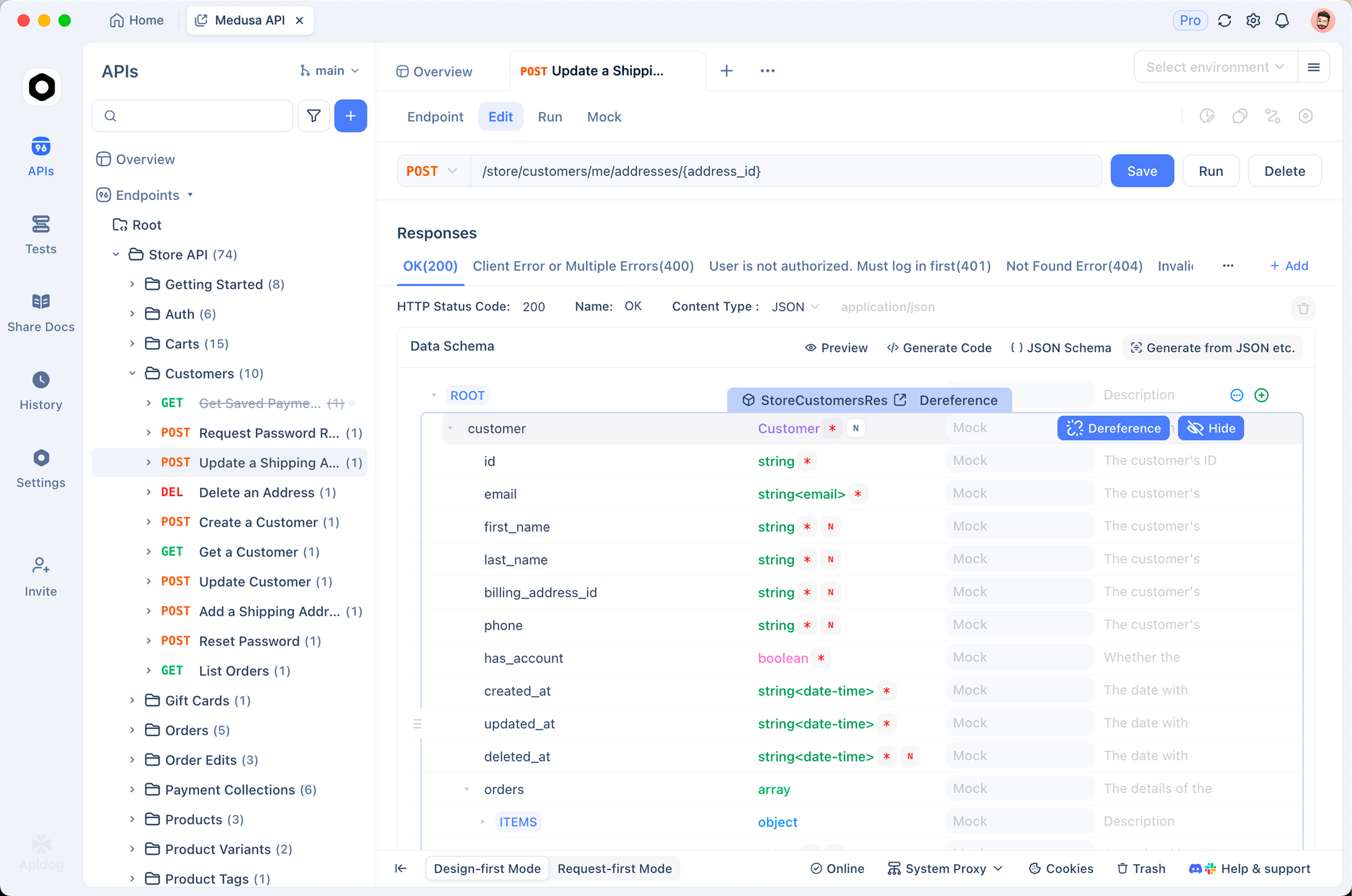
これを促進するために、API管理ツールとの統合は非常に貴重です。例えば、ApidogはDeepSeekMath-V2エンドポイントのシームレスなテストを可能にします。ユーザーは証明生成リクエスト用のAPIスキーマを設計し、検証メタデータを含むモック応答を作成し、リアルタイムダッシュボードでレイテンシを監視できます。このセットアップはプロトタイピングを加速します。Hugging Faceモデルをインポートし、FastAPI経由で公開し、Apidogの契約テストで検証します。
企業環境では、このような統合はバッチ検証を処理するために拡張され、Apidogのキャッシングレイヤーを通じて計算オーバーヘッドを削減します。したがって、DeepSeekMath-V2は研究成果物から生産資産へと移行します。
比較と限界:AIエコシステムにおけるDeepSeekMath-V2の位置づけ
DeepSeekMath-V2は、数学に特化したタスクにおいて、Llama-3.1-405Bのようなオープンソースの競合モデルを上回り、証明の正確性で15~20%の向上を達成しています。クローズドモデルと比較しても、検証が重視されるベンチマークでは差を詰めていますが、多言語サポートでは遅れを取っています。Apache 2.0ライセンスはアクセスを民主化し、プロプライエタリな制限とは対照的です。
しかし、限界は残っています。高いパラメータ数は、推論にかなりのVRAM(最低8x A100 GPU)を必要とします。検証計算は長い証明のレイテンシを増大させ、モデルは形式的な構造を持たない学際的な問題に苦戦します。将来のイテレーションでは、蒸留技術を通じてこれらに対応する可能性があります。
それにもかかわらず、これらのトレードオフは比類のない信頼性をもたらし、DeepSeekMath-V2を検証可能なAIの基礎として位置付けています。
将来の方向性:DeepSeekMath-V2による数学AIの進化
今後、DeepSeekMath-V2は、証明に図を組み込むマルチモーダル推論への道を開きます。形式検証コミュニティとの連携により、CoqやIsabelleのエコシステムに組み込まれる可能性があります。さらに、RLの進歩は検証器の進化を自動化し、人間の監視を最小限に抑えるかもしれません。
要約すると、DeepSeekMath-V2は自己検証可能なメカニズムを通じて数学AIを再定義します。そのアーキテクチャ、トレーニング、およびパフォーマンスは、Apidogのようなツールによって強化され、より広範な採用を促します。AIが成熟するにつれて、このようなモデルは推論が真実に基づいていることを保証します。
