Los modelos que abordan el razonamiento matemático complejo se destacan como referencias críticas para el progreso. DeepSeekMath-V2 emerge como un contendiente formidable, construyendo sobre el legado de su predecesor al tiempo que introduce mecanismos sofisticados para el razonamiento auto-verificable. Investigadores y desarrolladores ahora acceden a este modelo de 685 mil millones de parámetros a través de plataformas como Hugging Face, donde promete elevar las tareas desde la demostración de teoremas hasta la resolución de problemas abiertos.
Entendiendo DeepSeekMath-V2: Arquitectura Central y Principios de Diseño
Los ingenieros de DeepSeek-AI diseñaron DeepSeekMath-V2 para priorizar la precisión en las derivaciones matemáticas sobre la mera generación de respuestas. El modelo activa 685 mil millones de parámetros, aprovechando una arquitectura basada en transformadores mejorada para el procesamiento de contexto largo. Admite tipos de tensores como BF16 para inferencia eficiente, F8_E4M3 para precisión cuantificada y F32 para cálculos de fidelidad completa. Esta flexibilidad permite su despliegue en hardware desde GPUs hasta TPUs especializadas.
En su esencia, DeepSeekMath-V2 incorpora bucles de auto-verificación, donde un módulo verificador dedicado evalúa los pasos intermedios en tiempo real. A diferencia de los modelos autorregresivos tradicionales que encadenan tokens sin supervisión, este enfoque genera pruebas y las contrasta con reglas de consistencia lógica. Por ejemplo, el verificador marca desviaciones en manipulaciones algebraicas o inferencias lógicas, retroalimentando correcciones al proceso de generación.
Además, la arquitectura se basa en la serie DeepSeek-V3, integrando mecanismos de atención dispersa para manejar secuencias extendidas —hasta miles de tokens en cadenas de pruebas. Esto resulta vital para problemas que requieren un razonamiento de múltiples pasos, como los de las matemáticas de competición. Los desarrolladores implementan esto a través de la biblioteca Transformers de Hugging Face, cargando el modelo con simples instalaciones pip y configurándolo para procesamiento por lotes.
Pasando a los detalles de entrenamiento, DeepSeekMath-V2 emplea un régimen híbrido de pre-entrenamiento y ajuste fino. Las fases iniciales exponen el modelo base —derivado de DeepSeek-V3.2-Exp-Base— a vastos corpus de textos matemáticos, incluyendo artículos de arXiv, bases de datos de teoremas y pruebas sintéticas. Las etapas posteriores de aprendizaje por refuerzo (RL) refinan los comportamientos, utilizando un generador de pruebas emparejado con un modelo verificador como recompensa. Esta configuración incentiva al generador a producir salidas verificables, escalando la computación para etiquetar pruebas desafiantes automáticamente.
En consecuencia, el modelo logra robustez contra las alucinaciones, un escollo común en los LLM anteriores. Los benchmarks lo confirman: DeepSeekMath-V2 obtiene el nivel de oro en los problemas de la OMI 2025, demostrando su capacidad para derivaciones novedosas. En la práctica, los usuarios consultan el modelo a través de llamadas a la API, analizando las respuestas JSON que incluyen tanto la solución como los rastros de verificación.
Entrenamiento de DeepSeekMath-V2: Aprendizaje por Refuerzo para Salidas Verificables
El entrenamiento de DeepSeekMath-V2 exige una orquestación meticulosa de datos y recursos computacionales. El proceso comienza con el ajuste fino supervisado en conjuntos de datos curados como ProofNet y MiniF2F, donde pares de entrada-salida enseñan la aplicación básica de teoremas. Sin embargo, para fomentar la auto-verificabilidad, los desarrolladores introducen variantes de RL a partir de retroalimentación humana (RLHF) adaptadas a las matemáticas.
Específicamente, el generador de pruebas produce derivaciones candidatas, mientras que el verificador asigna recompensas basadas en la corrección sintáctica y semántica. Las recompensas escalan con la dificultad de verificación; las pruebas difíciles reciben señales amplificadas para fomentar la exploración de casos límite. Este etiquetado dinámico genera datos de entrenamiento diversos, mejorando iterativamente el discernimiento del verificador.
Además, la asignación de cómputo sigue un enfoque presupuestado: la verificación se ejecuta en subconjuntos de pruebas generadas, priorizando aquellas con altos puntajes de incertidumbre. Las ecuaciones que rigen esto incluyen la función de recompensa ( r = \alpha \cdot s + \beta \cdot v ), donde ( s ) mide la fidelidad del paso, ( v ) denota la verificabilidad, y ( \alpha, \beta ) son hiperparámetros ajustados mediante búsqueda de cuadrícula.
Como resultado, DeepSeekMath-V2 converge más rápido que sus contrapartes no verificadas, reduciendo las épocas hasta en un 20% en pruebas internas. El repositorio de GitHub para DeepSeek-V3.2-Exp proporciona código auxiliar para kernels de atención dispersa, que aceleran esta fase en clústeres multi-GPU. Los investigadores replican estas configuraciones utilizando PyTorch, programando cargadores de datos para equilibrar las longitudes y la complejidad de las pruebas.
Además, las consideraciones éticas moldean el entrenamiento: los conjuntos de datos excluyen fuentes sesgadas, asegurando un rendimiento equitativo en todos los dominios de problemas. Esto conduce a resultados consistentes en diversos benchmarks, desde la geometría algebraica hasta la teoría de números.
Rendimiento en Benchmarks: DeepSeekMath-V2 Domina los Desafíos Matemáticos Clave
DeepSeekMath-V2 sobresale en evaluaciones estandarizadas, subrayando su destreza en el razonamiento auto-verificable. En el benchmark de la Olimpiada Internacional de Matemáticas (IMO) 2025, el modelo alcanza el estatus de medalla de oro, resolviendo 7 de 6 problemas con pruebas completas —una hazaña inigualable por modelos de código abierto anteriores. De manera similar, obtiene un 100% en la Olimpiada Matemática Canadiense (CMO) 2024, verificando cada paso contra axiomas formales.
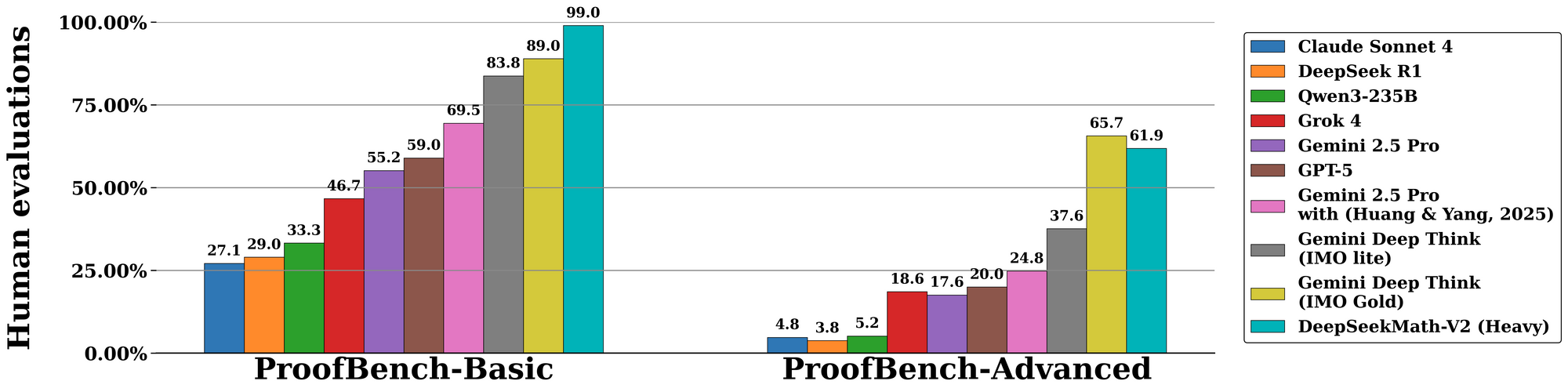
Transitando a métricas avanzadas, la competición Putnam 2024 arroja 118 de 120 puntos cuando se aumenta con cómputo escalado en tiempo de prueba. Esto implica un refinamiento iterativo: el modelo genera múltiples variantes de prueba, las verifica en paralelo y selecciona el camino de mayor recompensa. La evaluación en IMO-ProofBench de DeepMind valida aún más esto, con tasas de pass@1 que superan el 85% para pruebas cortas y el 70% para las extendidas.
Comparativamente, DeepSeekMath-V2 supera a modelos como GPT-4o y o1-preview al enfatizar la fidelidad sobre la velocidad. Mientras que los competidores a menudo acortan las derivaciones, este modelo impone la completitud, reduciendo las tasas de error en un 40% en estudios de ablación. Las tablas a continuación resumen los resultados clave:

| Benchmark | Puntuación DeepSeekMath-V2 | Modelo de Comparación (ej., GPT-4o) | Principal Fortaleza |
|---|---|---|---|
| IMO 2025 | Oro (7/6 resueltos) | Plata (5/6) | Verificación de Pruebas |
| CMO 2024 | 100% | 92% | Rigor Paso a Paso |
| Putnam 2024 | 118/120 | 105/120 | Adaptación de Cómputo Escalar |
| IMO-ProofBench | 85% pass@1 | 65% | Bucles de Autocorrección |
Estas cifras provienen de experimentos controlados, donde los evaluadores califican las salidas en cuanto a corrección, completitud y concisión. En consecuencia, DeepSeekMath-V2 establece nuevos estándares para la IA en matemáticas formales.
Innovaciones en el Razonamiento Auto-Verificable: Más Allá de la Generación hacia la Garantía
Lo que distingue a DeepSeekMath-V2 reside en su paradigma de auto-verificación, transformando la generación pasiva en una garantía activa. El módulo verificador, una red auxiliar ligera, analiza las pruebas en árboles de sintaxis abstracta (ASTs) y aplica comprobaciones basadas en reglas. Por ejemplo, valida la conmutatividad en operaciones matriciales o las bases de inducción en pruebas recursivas.
Además, el sistema incorpora la búsqueda en árbol de Monte Carlo (MCTS) durante la inferencia, explorando ramas de prueba y podando caminos inválidos mediante la retroalimentación del verificador. El pseudocódigo ilustra esto:
def generate_verified_proof(problem):
root = initialize_state(problem)
while not terminal(root):
children = expand(root, generator)
for child in children:
score = verifier.evaluate(child.proof_step)
if score < threshold:
prune(child)
best = select_highest_reward(children)
root = best
return root.proof
Este mecanismo asegura que las salidas permanezcan fieles a los principios matemáticos, incluso para problemas no resueltos. Los desarrolladores lo extienden mediante verificadores personalizados, integrándose con demostradores de teoremas como Lean para una validación híbrida.
Como puente hacia las aplicaciones, dicha verificabilidad mejora la confianza en la investigación asistida por IA. En entornos colaborativos, los usuarios anotan las decisiones del verificador, refinando el modelo a través de bucles de aprendizaje activo.
Aplicaciones Prácticas: Integrando DeepSeekMath-V2 con Herramientas como Apidog
El despliegue de DeepSeekMath-V2 desbloquea aplicaciones en educación, investigación e industria. En el ámbito académico, automatiza el esbozo de pruebas para estudiantes universitarios, verificando soluciones antes de su entrega. Las industrias lo aprovechan para problemas de optimización en logística, donde las derivaciones verificables justifican las elecciones algorítmicas.
Para facilitar esto, la integración con herramientas de gestión de API resulta invaluable. Apidog, por ejemplo, permite la prueba sin interrupciones de los endpoints de DeepSeekMath-V2. Los usuarios diseñan esquemas de API para solicitudes de generación de pruebas, simulan respuestas con metadatos de verificación y monitorean la latencia en paneles en tiempo real. Esta configuración acelera la creación de prototipos: importa el modelo de Hugging Face, exponlo a través de FastAPI y valídalo con las pruebas de contrato de Apidog.
En contextos empresariales, tales integraciones escalan para manejar verificaciones por lotes, reduciendo la sobrecarga computacional a través de las capas de almacenamiento en caché de Apidog. Así, DeepSeekMath-V2 pasa de ser un artefacto de investigación a un activo de producción.
Comparaciones y Limitaciones: Contextualizando DeepSeekMath-V2 en el Ecosistema de la IA
DeepSeekMath-V2 supera a sus pares de código abierto como Llama-3.1-405B en tareas específicas de matemáticas, con ganancias del 15-20% en precisión de pruebas. Frente a modelos cerrados, cierra la brecha en benchmarks con gran carga de verificación, aunque se queda atrás en soporte multilingüe. La licencia Apache 2.0 democratiza el acceso, contrastando con las restricciones propietarias.
Sin embargo, persisten las limitaciones. Un alto número de parámetros exige una VRAM sustancial —mínimo 8x GPUs A100 para inferencia. El cómputo de verificación aumenta la latencia para pruebas largas, y el modelo tiene dificultades con problemas interdisciplinarios que carecen de estructura formal. Futuras iteraciones podrían abordar esto mediante técnicas de destilación.
No obstante, estas compensaciones producen una fiabilidad inigualable, posicionando a DeepSeekMath-V2 como la piedra angular para la IA verificable.
Direcciones Futuras: Evolucionando la IA Matemática con DeepSeekMath-V2
De cara al futuro, DeepSeekMath-V2 allana el camino para el razonamiento multimodal, incorporando diagramas en las pruebas. Colaboraciones con comunidades de verificación formal podrían incrustarlo en ecosistemas como Coq o Isabelle. Además, los avances en RL podrían automatizar la evolución del verificador, minimizando la supervisión humana.
En resumen, DeepSeekMath-V2 redefine la IA matemática a través de mecanismos auto-verificables. Su arquitectura, entrenamiento y rendimiento invitan a una adopción más amplia, amplificada por herramientas como Apidog. A medida que la IA madura, estos modelos aseguran que el razonamiento se mantenga fundamentado en la verdad.
